A compreensão dos algoritmos de ordenação é essencial na ciência da computação, ensinando-nos sobre eficiência, uso de memória e estratégias de resolução de problemas. Cada algoritmo, desde os simples como Selection Sort e Bubble Sort até os mais eficientes como Merge Sort e Quick Sort, oferece insights valiosos sobre como abordagens diferentes podem impactar o desempenho da ordenação de dados. Estudar esses algoritmos não apenas melhora nossa habilidade de organizar dados de forma eficaz, mas também desenvolve uma mentalidade analítica aplicável a uma ampla gama de desafios computacionais.

Esta jornada no mundo dos algoritmos de ordenação é uma porta de entrada para aprimorar a habilidade de pensar criticamente e resolver problemas complexos, fundamentos que vão muito além da simples ordenação de elementos.

Para uma visão mais aprofundada e visual dos diferentes algoritmos de ordenação em ação, confira este vídeo que apresenta uma variedade de métodos de ordenação, observe quantas comparações e acessos cada método faz:

O algoritmo de selection sort organiza uma lista selecionando repetidamente o elemento mínimo da parte desordenada e movendo-o para a posição inicial dessa parte.

O objetivo deste exercício é visualizar como a lista original é modificada ao longo das iterações do algoritmo, oferecendo uma perspectiva clara do processo de ordenação passo a passo.

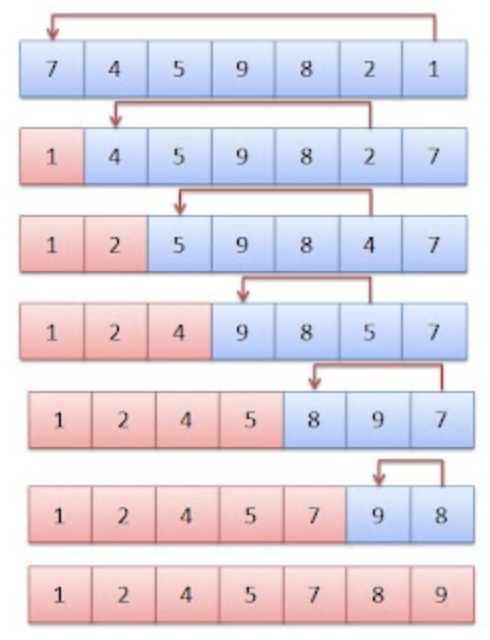
Na imagem acima, você encontra uma ilustração do algoritmo em funcionamento.

Entrada Uma lista de inteiros desordenada.

Saída: Uma lista de listas, onde cada sublista mostra o estado da lista original após cada iteração do processo de seleção e troca.

    selection_sort_steps([3, 1, 2]) >> [[1, 3, 2], [1, 2, 3]] 
selection_sort_steps([4, 3, 2, 1]) >>[[1, 3, 2, 4], [1, 2, 3, 4] ]
selection_sort_steps([2, 3, 1, 5, 4]) == [[1, 3, 2, 5, 4], [1, 2, 3, 5, 4], [1, 2, 3, 4, 5]]