
Flip of Time

An hourglass is given as a tuple (upper, lower) for the number of minutes of sand that are currently stored in its upper and lower chambers, both chambers large enough to hold all of the sand in that hourglass. So after m minutes of time has elapsed, the state of that particular hourglass will be upper - min(upper, m), lower + min(upper, m). The total amount of sand inside the hourglass never changes, nor will either chamber ever contain negative anti-sand.
Given a list of glasses, your task is to find an optimal sequence of moves to measure exactly t minutes, scored as the number of individual hourglass flips performed along the way. Each move consists of two stages:
- you must first wait for the hourglass that currently holds the lowest non zero amount m of sand in its upper chamber to run out.
- when that happens, choose any subset of glasses and instantaneously flip this chosen subset.
Look at the example for [(7, 0), (11, 0)], 15 case. You can find an explanation for slightly changed case in a Popular Mechanics article.
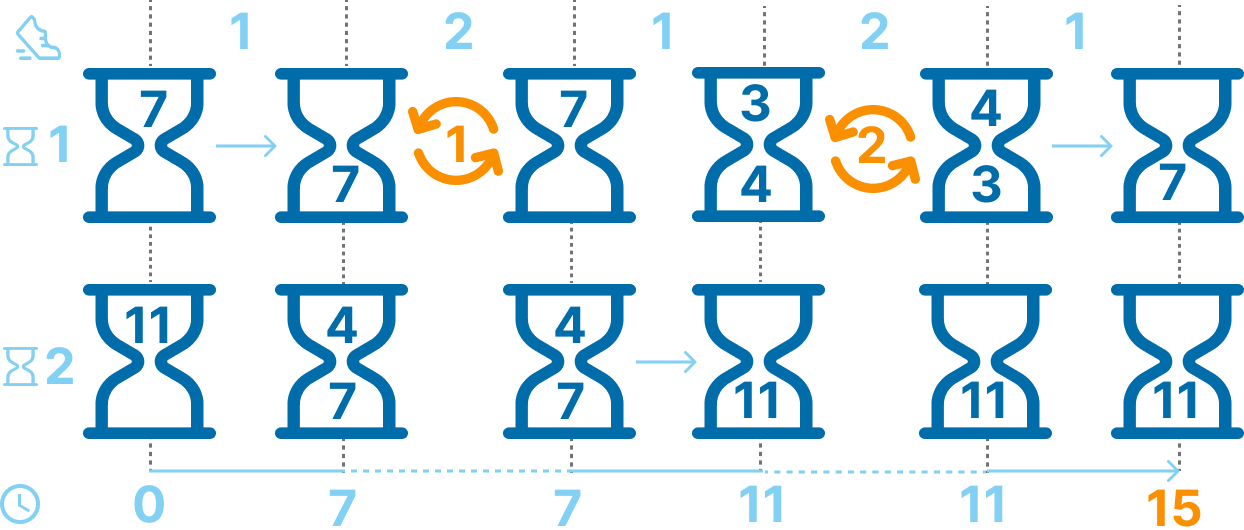
You don’t have any choice in waiting in the first stage, but in the second stage you enjoy an embarrassment of riches of 2n – 1 possible moves for n glasses!
This function should return the smallest possible number of individual hourglass flips needed to measure exactly t minutes, or None if this exact measurement is impossible.
Input: Two arguments: list of tuples of two integers (int), integer.
Output: Integer or None.
Examples:
assert hourglass_flips([(1, 0), (2, 0)], 2) == 0 assert hourglass_flips([(7, 0), (11, 0)], 15) == 2 assert hourglass_flips([(4, 0), (6, 0)], 11) == None assert hourglass_flips([(7, 1), (10, 4), (13, 1), (18, 4)], 28) == 3
Pss..if you feel yourself in need of a hint, click this line.
The base cases of recursion are when t equals 0 or when exactly t minutes remain in some upper chamber (no flips are needed), or when t is smaller than the smallest time remaining in the upper chamber of any hourglass (no solution is possible). Otherwise, update all hourglasses to their new states after m minutes, and loop through all possible subsets of glasses to flip. For each such subset, recursively construct the optimal sequence of moves to measure the remaining t - m minutes, and combine these moves to the best solution.
The mission was taken from Python CCPS 109. It is taught for Ryerson Chang School of Continuing Education by Ilkka Kokkarinen
CheckiO Extensions allow you to use local files to solve missions. More info in a blog post.
In order to install CheckiO client you'll need installed Python (version at least 3.8)
Install CheckiO Client first:
pip3 install checkio_client
Configure your tool
checkio --domain=py config --key=
Sync solutions into your local folder
checkio sync
(in beta testing) Launch local server so your browser can use it and sync solution between local file end extension on the fly. (doesn't work for safari)
checkio serv -d
Alternatevly, you can install Chrome extension or FF addon
checkio install-plugin
checkio install-plugin --ff
checkio install-plugin --chromium
Read more here about other functionality that the checkio client provides. Feel free to submit an issue in case of any difficulties.
Welcome to Pair Programming! Engage in real-time collaboration on coding projects by starting a session and sharing the provided unique URL with friends or colleagues. This feature is perfect for joint project development, debugging, or learning new skills together. Simply click 'Start Session' to begin your collaborative coding journey!
You are trying to join a pair programming session that has not started yet.
Please wait for the session creator to join.
It looks like the creator of the pair programming session closed the editor window.
It might happen accidentally, so that you can wait for reconnection.
