Fibonacci Spiral's End
I believe, you have heard about Fibonacci numbers, which form a respective sequence, where each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
|
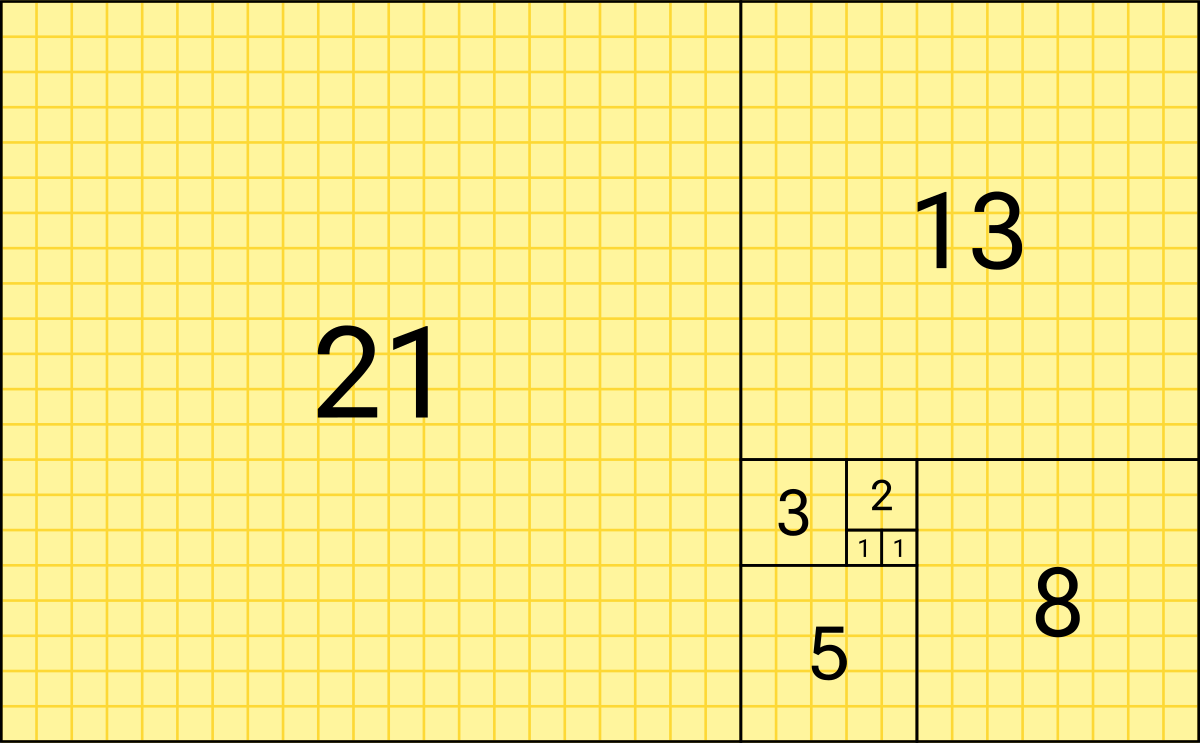
The sequence may be shown as a tiling with squares whose side lengths are successive Fibonacci numbers. For this mission we use exactly this position of squares: |
If you follow numbers, you see that they form a spiral. Indeed, on the next image the Fibonacci spiral is build: an approximation of the golden spiral, created by drawing circular arcs, connecting the opposite corners of squares in the Fibonacci tiling: |
Now let's put x-axis and y-axis on the image with 0 point in the start of the spiral. Each numbered dot marked is the corner of the square (or the very start of the spiral) of i-th number, where the spiral ends if i-th number is the last one:

So, for the given sequence number, your function should return the coordinates [x, y] of the end of the spiral (square corner) for the respective Fibonacci number. let's look at the table:
| Sequence number (function input) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Respective Fibonacci number | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | ... | ||||||||||
| Coordinates of the corner (spiral's end) | [0, 0] | [1, -1] | [2, 0] | [0, 2] | [-3, -1] | [2, -6] | [10, 2] | [-3, 15] | [-24, -6] | ... |
Input: Integer.
Output: List of two integers.
Examples:
assert fibo_spiral_end(0) == [0, 0] assert fibo_spiral_end(1) == [1, -1] assert fibo_spiral_end(2) == [2, 0] assert fibo_spiral_end(3) == [0, 2]

How it’s used: Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the Fibonacci Quarterly. Applications of Fibonacci numbers include computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure, and graphs called Fibonacci cubes used for interconnecting parallel and distributed systems. They also appear in biological settings, such as branching in trees, the arrangement of leaves on a stem, the fruit sprouts of a pineapple, the flowering of an artichoke, an uncurling fern, and the arrangement of a pine cone's bracts.
CheckiO Extensions allow you to use local files to solve missions. More info in a blog post.
In order to install CheckiO client you'll need installed Python (version at least 3.8)
Install CheckiO Client first:
pip3 install checkio_client
Configure your tool
checkio --domain=py config --key=
Sync solutions into your local folder
checkio sync
(in beta testing) Launch local server so your browser can use it and sync solution between local file end extension on the fly. (doesn't work for safari)
checkio serv -d
Alternatevly, you can install Chrome extension or FF addon
checkio install-plugin
checkio install-plugin --ff
checkio install-plugin --chromium
Read more here about other functionality that the checkio client provides. Feel free to submit an issue in case of any difficulties.
Welcome to Pair Programming! Engage in real-time collaboration on coding projects by starting a session and sharing the provided unique URL with friends or colleagues. This feature is perfect for joint project development, debugging, or learning new skills together. Simply click 'Start Session' to begin your collaborative coding journey!
You are trying to join a pair programming session that has not started yet.
Please wait for the session creator to join.
It looks like the creator of the pair programming session closed the editor window.
It might happen accidentally, so that you can wait for reconnection.