Inscribe a Contour
Over the past almost 15 years, 3D printing has become very popular, not only amongst the big industrial companies which can afford to buy a super expensive 3D manufacturing complex (e.i. SLM or SLS machines), but also among ordinary people, engineers and enthusiasts. It started in 2005 with the RepRap project within the University of Bath. The project's main objective was to develop an affordable production system that would enable the production of cheap everyday household goods regardless of the household's location. The project was successful and gave birth to the printer called "Darwin" at the beginning of 2008. It was a fully open project under the GNU GPL and by the end of 2008th ~100 copies of "Darwin" have been produced in various countries. Since then, there has been an exponential increase in the number of printers manufactured, both DIY and commercial. Most of the FDM printers you may find today in libraries, universities, workshops, engineering companies, friend's houses are likely to be direct descendants of that very first desktop printer. I do not possess any more up to date information, but in 2013 it's been sold ~72.000 of desktop printers, in 2014 - almost 140.000 (according to the Wohlers Report ).

Leaving aside the 3D design process, which is the first step on the way to something to be printed, we go straight to preparing a 3D model for printing. There's a variety of software applications designed for that purpose called slicers . They slice a 3D model from the bottom to the top with a constant (not always) height and get a sequence of the planar contours, each of which is represented by a sequence of the dots.

These sequences of dots then, obvious, are used for a printing program along with the calculated velocities, accelerations, etc.
In order to estimate if a model fits the printer
building table (video)
and then can be printed, our slicing software should find the optimal orientation of the model on the table, so the model will require the least possible space.
So, in this mission you are given a list of dots, each represents a projection of a 3D model vertex onto a horizontal plane.
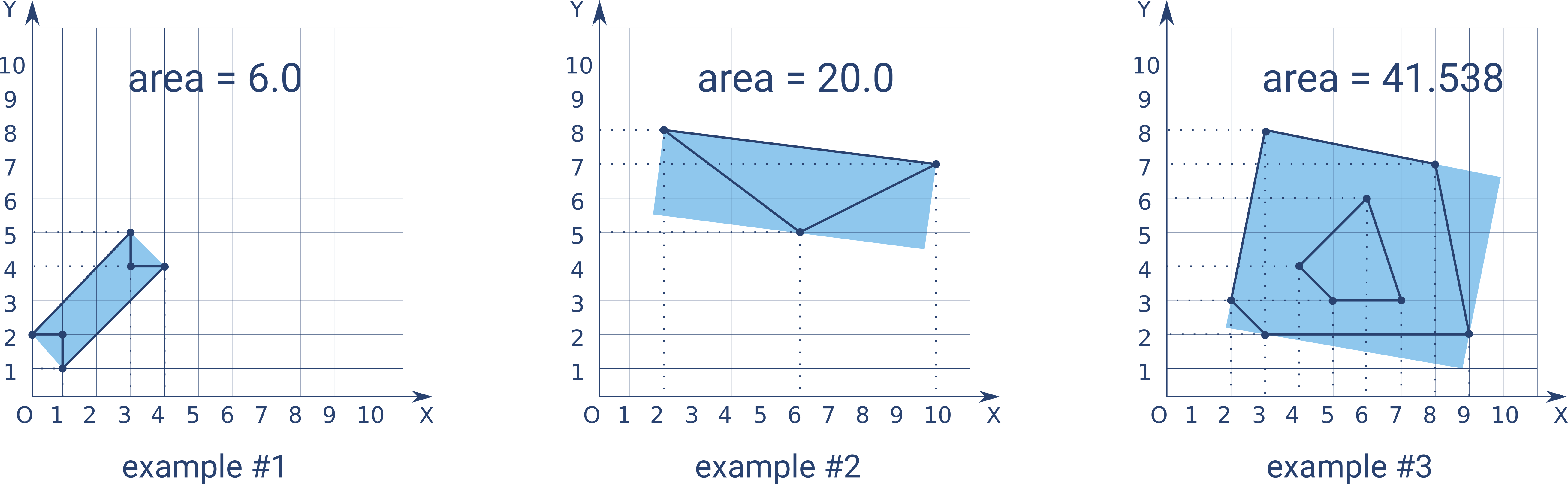
Your task is to find the smallest rectangle (by its area) into which all the given dots (and thus the projected contour) can be inscribed.
Input: A list of tuples, each tuple contains coordinates of a projected dot (x, y). All given coordinates are integers. Although in the example illustrations the dots are connected, forming sane contours, they can be connected in any arbitrary consequence and that won't affect the result.
Output: The area of the smallest rectangle (with ±0.001 precision) which inscribes the given contour.
Example:
inscribe([(1, 1), (1, 2), (0, 2), (3, 5), (3, 4), (4, 4)]) == 6.0 #example #1
inscribe([(6, 5), (10, 7), (2, 8)]) == 20.0 #example #2
inscribe([(2, 3), (3, 8), (8, 7), (9, 2), (3, 2), (4, 4), (6, 6), (7, 3), (5, 3)]) == 41.538 #example #3
Precondition:
- n ∈ [3; 30] - dots number
- i = range(n)
- x i ∈ [0; 300] - x coordinate of the i-th dot
- y i ∈ [0; 300] - y coordinate of the i-th dot
- there won't be two (or more) similar dots
- there won't be a case with all the dots on the same line
CheckiO Extensions allow you to use local files to solve missions. More info in a blog post.
In order to install CheckiO client you'll need installed Python (version at least 3.8)
Install CheckiO Client first:
pip3 install checkio_client
Configure your tool
checkio --domain=py config --key=
Sync solutions into your local folder
checkio sync
(in beta testing) Launch local server so your browser can use it and sync solution between local file end extension on the fly. (doesn't work for safari)
checkio serv -d
Alternatevly, you can install Chrome extension or FF addon
checkio install-plugin
checkio install-plugin --ff
checkio install-plugin --chromium
Read more here about other functionality that the checkio client provides. Feel free to submit an issue in case of any difficulties.
Welcome to Pair Programming! Engage in real-time collaboration on coding projects by starting a session and sharing the provided unique URL with friends or colleagues. This feature is perfect for joint project development, debugging, or learning new skills together. Simply click 'Start Session' to begin your collaborative coding journey!
You are trying to join a pair programming session that has not started yet.
Please wait for the session creator to join.
It looks like the creator of the pair programming session closed the editor window.
It might happen accidentally, so that you can wait for reconnection.
